All About Triangles And Quadrilaterals: Essential Guide To 2D Geometric Shapes

What are "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:"?

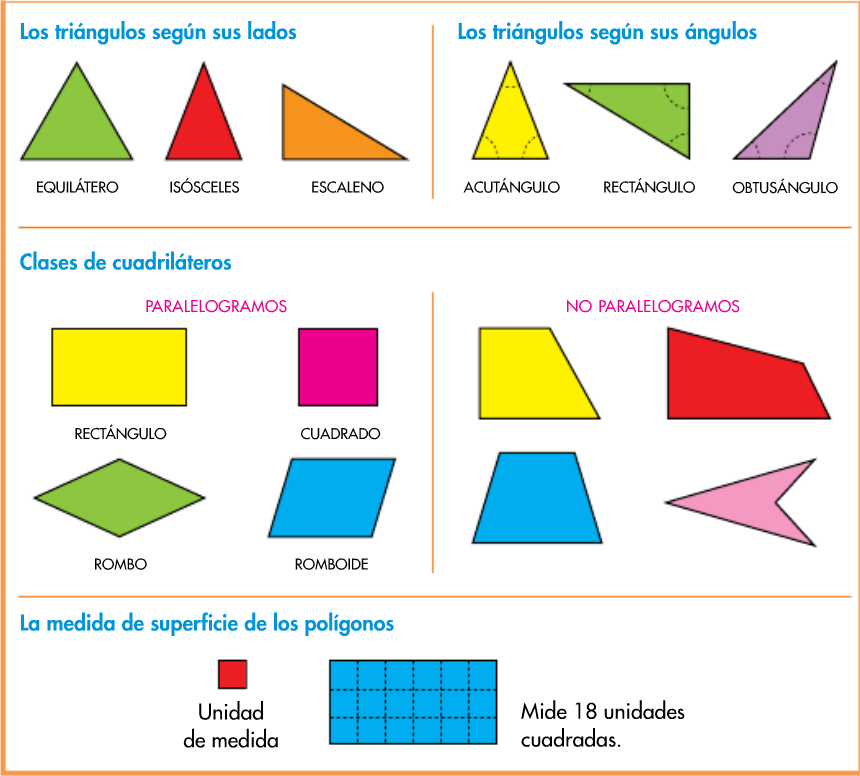
Figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros are two-dimensional shapes that are defined by their sides and angles. Triangles have three sides and three angles, while quadrilaterals have four sides and four angles.

Triangles and quadrilaterals are two of the most basic geometric shapes and are used in a wide variety of applications, from architecture to engineering to art. Triangles are strong and stable, making them ideal for use in structures such as bridges and buildings. Quadrilaterals are also versatile shapes, and can be used to create a variety of different objects, such as boxes, frames, and wheels.

The study of figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros is called geometry. Geometry is a branch of mathematics that deals with the properties of shapes and their relationships to each other.

Geometry is an important subject for students to learn because it helps them to develop their spatial reasoning skills. Spatial reasoning skills are essential for success in a variety of fields, including science, technology, engineering, and mathematics.

Figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros

Sides: Triangles have three sides, while quadrilaterals have four sides.
Angles: Triangles have three angles, while quadrilaterals have four angles.
Shape: Triangles are typically triangular in shape, while quadrilaterals can be square, rectangular, or trapezoidal.
Area: The area of a triangle is calculated by multiplying the base by the height and dividing by two. The area of a quadrilateral is calculated by multiplying the length by the width.
Perimeter: The perimeter of a triangle is the sum of the lengths of its three sides. The perimeter of a quadrilateral is the sum of the lengths of its four sides.

These are just a few of the key aspects of figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros. These shapes are used in a wide variety of applications, from architecture to engineering to art. By understanding the properties of these shapes, you can better understand the world around you.

Sides

The number of sides is a key defining characteristic of both triangles and quadrilaterals. Triangles, as their name suggests, have three sides, while quadrilaterals have four sides. This difference in the number of sides has a significant impact on the properties of these shapes.

For example, triangles are inherently more stable than quadrilaterals because they have fewer sides. This makes them ideal for use in structures such as bridges and buildings. Quadrilaterals, on the other hand, are more versatile than triangles because they can be used to create a wider variety of shapes and objects.

The number of sides of a shape also affects its area and perimeter. For example, a triangle with a base of 10 cm and a height of 8 cm will have an area of 40 cm². A quadrilateral with the same base and height will have an area of 80 cm². This is because the quadrilateral has more sides, which means that it has a larger perimeter.

Understanding the relationship between the number of sides and the properties of shapes is essential for anyone who works with geometry. This understanding can be applied to a wide range of fields, including architecture, engineering, and design.

Angles

The number of angles is another key defining characteristic of both triangles and quadrilaterals. Triangles, as their name suggests, have three angles, while quadrilaterals have four angles. This difference in the number of angles has a significant impact on the properties of these shapes.

For example, the sum of the interior angles of a triangle is always 180 degrees. This is because the interior angles of a triangle are formed by three straight lines, and the sum of the interior angles of a straight line is always 180 degrees. The sum of the interior angles of a quadrilateral, on the other hand, is always 360 degrees. This is because the interior angles of a quadrilateral are formed by four straight lines, and the sum of the interior angles of a straight line is always 180 degrees.

The number of angles of a shape also affects its shape and stability. For example, triangles are inherently more stable than quadrilaterals because they have fewer angles. This makes them ideal for use in structures such as bridges and buildings. Quadrilaterals, on the other hand, are more versatile than triangles because they can be used to create a wider variety of shapes and objects.

Understanding the relationship between the number of angles and the properties of shapes is essential for anyone who works with geometry. This understanding can be applied to a wide range of fields, including architecture, engineering, and design.

Shape

The shape of a figure is one of its most important characteristics. Triangles are typically triangular in shape, while quadrilaterals can be square, rectangular, or trapezoidal.

Triangles are three-sided figures with three angles. They are typically triangular in shape, but they can also be equilateral (all sides are equal), isosceles (two sides are equal), or scalene (no sides are equal).
Quadrilaterals are four-sided figures with four angles. They can be square, rectangular, or trapezoidal. Squares have four equal sides and four right angles. Rectangles have four right angles, but their sides are not all equal. Trapezoids have one pair of parallel sides.

The shape of a figure can have a significant impact on its properties. For example, triangles are strong and stable, while quadrilaterals are more versatile. Triangles are often used in construction and engineering, while quadrilaterals are often used in art and design.

Area

The area of a figure is a measure of its two-dimensional size. It is calculated by multiplying the length of the figure by its width. In the case of a triangle, the base is the length of one of the sides of the triangle, and the height is the length of a line segment drawn from the vertex of the triangle to the base. In the case of a quadrilateral, the length is the length of one of the sides of the quadrilateral, and the width is the length of the side opposite the length.

Calculating the Area of a Triangle
The area of a triangle can be calculated using the following formula:$$A = \frac{bh}{2}$$where: A is the area of the triangle b is the length of the base of the triangle h is the height of the triangle
For example, if a triangle has a base of 10 cm and a height of 8 cm, then its area would be:$$A = \frac{(10 cm)(8 cm)}{2} = 40 cm^2$$
Calculating the Area of a Quadrilateral
The area of a quadrilateral can be calculated using the following formula:$$A = lw$$where: A is the area of the quadrilateral l is the length of the quadrilateral w is the width of the quadrilateral
For example, if a quadrilateral has a length of 10 cm and a width of 8 cm, then its area would be:$$A = (10 cm)(8 cm) = 80 cm^2$$

The area of a figure is an important property to know, as it can be used to calculate other properties of the figure, such as its volume or surface area.

Perimeter

The perimeter of a figure is a measure of its one-dimensional boundary. It is calculated by adding up the lengths of all of the sides of the figure. In the case of a triangle, the perimeter is the sum of the lengths of its three sides. In the case of a quadrilateral, the perimeter is the sum of the lengths of its four sides.

Importance of Perimeter
The perimeter of a figure is an important property to know, as it can be used to calculate other properties of the figure, such as its area or volume. For example, the perimeter of a rectangle can be used to calculate its area using the formula A = lw, where A is the area, l is the length, and w is the width.
Perimeter in Triangles and Quadrilaterals
The perimeter of a triangle is always less than the perimeter of a quadrilateral with the same side lengths. This is because triangles have fewer sides than quadrilaterals. For example, if a triangle has three sides of length 3 cm, 4 cm, and 5 cm, then its perimeter would be 12 cm. If a quadrilateral has four sides of length 3 cm, 4 cm, 5 cm, and 6 cm, then its perimeter would be 18 cm.
Applications of Perimeter
The perimeter of figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros is used in a wide variety of applications, including architecture, engineering, and manufacturing. For example, the perimeter of a room is used to calculate the amount of wallpaper needed to cover the walls. The perimeter of a pool is used to calculate the amount of fencing needed to surround the pool. The perimeter of a circuit board is used to calculate the amount of copper needed to make the board.

In conclusion, the perimeter of a figure is an important property to know, as it can be used to calculate other properties of the figure and has a wide variety of applications in the real world.

FAQs about Figuras Geometricas Planas Triangulos y Cuadrilateros Figuras Geometricas Planas Triangulos y Cuadrilateros

Question 1: What are the key differences between triangles and quadrilaterals?

Triangles have three sides and three angles, while quadrilaterals have four sides and four angles. Triangles are typically triangular in shape, while quadrilaterals can be square, rectangular, or trapezoidal.

Question 2: How do you calculate the area of a triangle?

The area of a triangle is calculated by multiplying the base by the height and dividing by two: A = (1/2) b h, where 'b' represents the length of the base, and 'h' represents the height or altitude of the triangle.

Question 3: What is the formula for finding the perimeter of a quadrilateral?

The perimeter of a quadrilateral is the sum of the lengths of all four sides: P = a + b + c + d, where 'a', 'b', 'c', and 'd' represent the lengths of each side.

Question 4: How are figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros used in real-life applications?

Triangles and quadrilaterals are widely used in architecture, engineering, and design. Triangles provide stability to structures due to their inherent strength, while quadrilaterals offer versatility in creating various shapes and objects.

Question 5: What are some examples of everyday objects with triangular or quadrilateral shapes?

Examples of triangular shapes include roof trusses, traffic signs, and pizza slices. Examples of quadrilateral shapes include books, windows, and tables.

Question 6: How can I improve my understanding of geometric shapes like triangles and quadrilaterals?

Practice drawing and identifying these shapes. Explore their properties and relationships through hands-on activities and problem-solving exercises.

In conclusion, understanding figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros is essential for grasping fundamental geometric concepts. Their applications extend beyond theoretical knowledge, as they play a significant role in various practical domains.

To learn more about geometric shapes and their applications, you can explore textbooks, online resources, or consult with educators in the field.

Conclusion

Figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros are fundamental geometric shapes with distinct properties and diverse applications. Triangles, characterized by three sides and three angles, exhibit inherent stability, making them suitable for structural support. Quadrilaterals, with their four sides and four angles, offer versatility in design and functionality.

Understanding the characteristics and relationships between triangles and quadrilaterals is essential for navigating the world of geometry. These shapes serve as building blocks for more complex figures and patterns, unlocking a deeper comprehension of spatial relationships and mathematical concepts.

Ultimate Guide To Writing Numbers In English From 1 To 1000
A History Of The Dutch East India Company: Rise And Fall Of A Global Trading Empire
A Comprehensive Guide To US Plug Electrical Standards: Your Ultimate Resource